藝術只可遠觀意會

一個機器學習有幾個要素，一群資料經過運算後衡量效果的好壞並不斷重複的過程。
而在前面的討論有提及，這個用來衡量的效果(Performance)，常常會改以損失函數(Loss Function)的形式來比較。

過擬合的問題，常常出現在過度解讀訓練資料，遇到測試資料就沒轍了。
課程中有提到奧卡姆剃刀原則：可以簡便，不要複雜。

但要注意，要運用這個原則是在可等價的情況下；不能的話也許就是所謂的取捨吧。

綜觀以上原則：
追求的目標需要改成：Minimize(Loss + Complexity)

而對應採用的方法我們就稱作Regularization：

• Early Stopping
• Norm Penalties
  • L1 regularization
  • L2 regularization
  • Max-norm regularization
    ...

L1可想成是LASSO，L2可想成是Ridge，而兩者綜合體想成Elastic-Net。

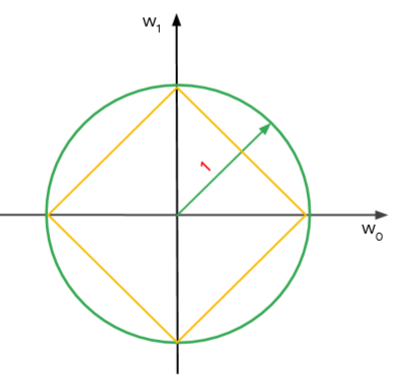
在計算正規處罰項目時，黃色可想成是L1規範區，綠色可想成是L2規範區。
我們可以發現，L2在處理系統的超參數時，由於移動路徑相切點是在圓上，變動幅度不大，可以取得相對來說比較穩定的解。
L1則因為快速的移動，不容易有相交的部分，解會比較不穩定；但也因為這個特性，L1能夠有效削減變數的數量，對於過擬合的情形能快速抑制。